自动驾驶规划算法 - A* 基本原理
版权声明:本文为 DLonng 非原创文章,可以随意转载,但必须在明确位置注明出处!
A* 发展过程
BFS
BFS 从起点开始,首先遍历起点周围邻居点,然后再遍历邻居的邻居,这样逐步的向外一层一层扩散(类似地震波),直到找到终点
-
时间复杂度:假设一个图有 N 个节点和 M 条边,BFS 会走遍所有节点,时间是 O(N),然后由于每个节点会检查所有的出边,最终所有的边都会被检查过,时间是 O(M) ,所以 BFS 的时间复杂度是 O(N+M)
-
空间复杂度:队列里面最多可能存放所有节点,空间复杂度为 O(N)

在上面这幅动态图中,BFS 算法遍历了图中所有的点,这通常没有必要,因为对于有明确终点的问题来说,一旦到达终点便可以提前终止算法。
Dijkstra
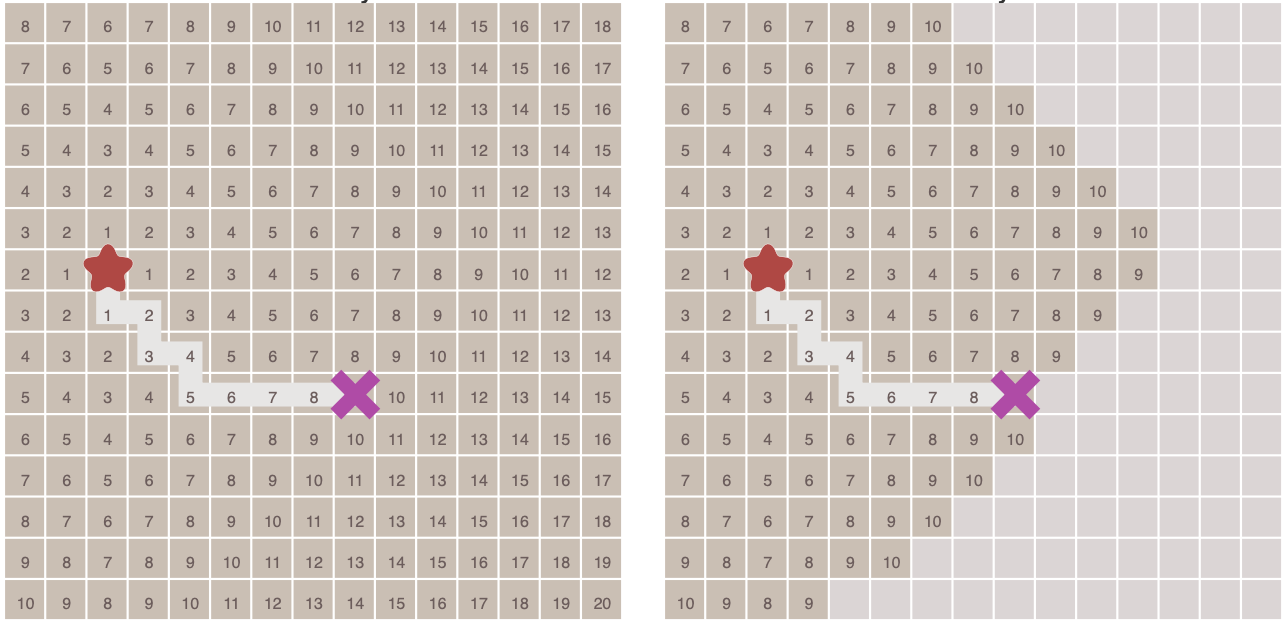
在一些情况下,图形中相邻节点之间的移动代价(边的权重)并不相等,Dijkstra 算法用来寻找图中移动代价不相同的节点之间的最短路径。
- 在算法中需要计算每一个节点距离起点的总移动代价(到起点的总权重),并把待遍历的节点加入优先队列中(按照代价排序),算法运行的过程中,每次都从优先队列中选出代价最小的作为下一个遍历的节点,直到到达终点为止
- 当图形为网格图,并且每个节点之间的移动代价相等,那么 Dijkstra 算法将和 BFS 一样
- 算法不知道目标节点的位置,因此它只能向所有可能的方向扩展节点直到发现目标节点为止
- 时间复杂度:不用最小优先队列 $O(V^2)$,用最小优先队列 $O((E + V)logV)$ (不太确定)

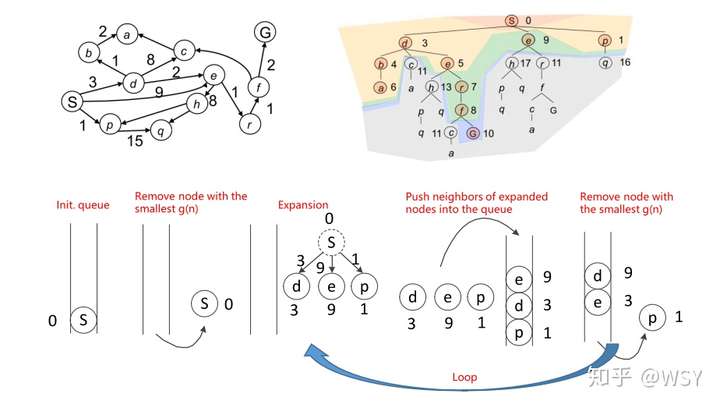
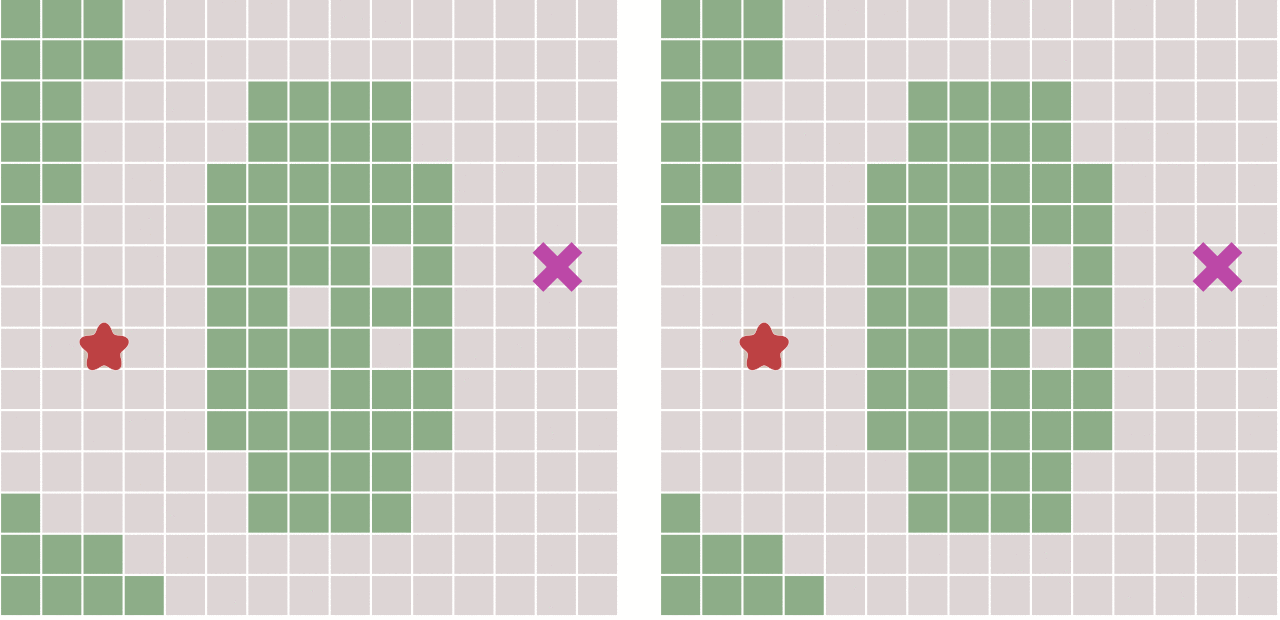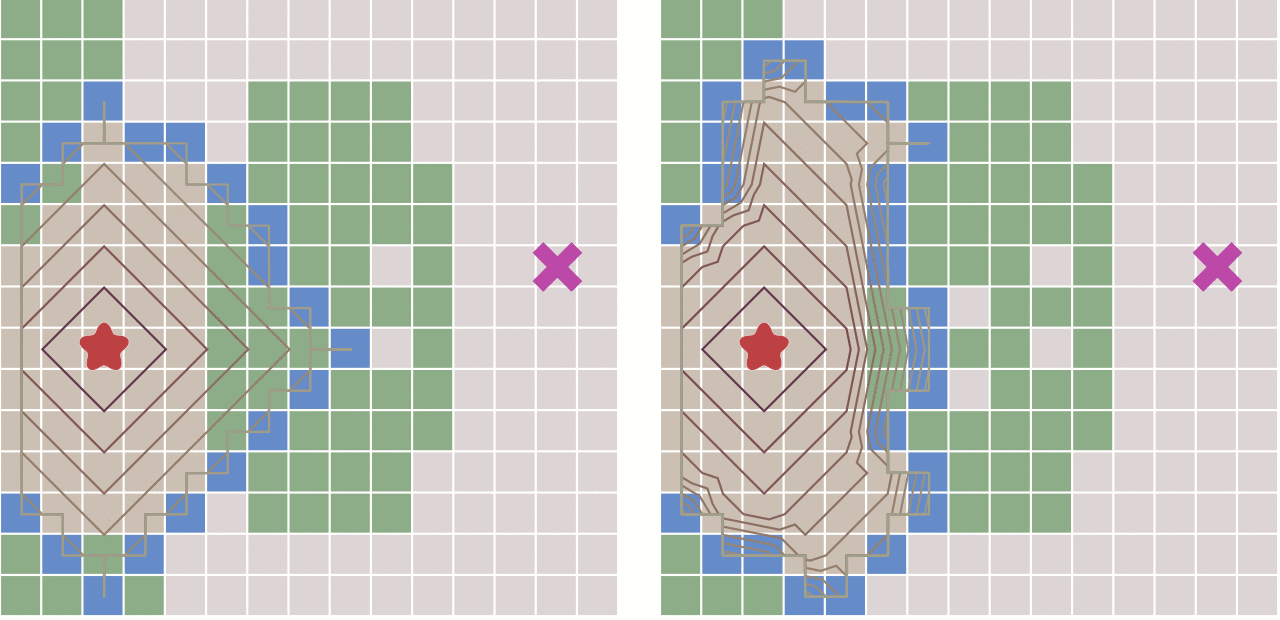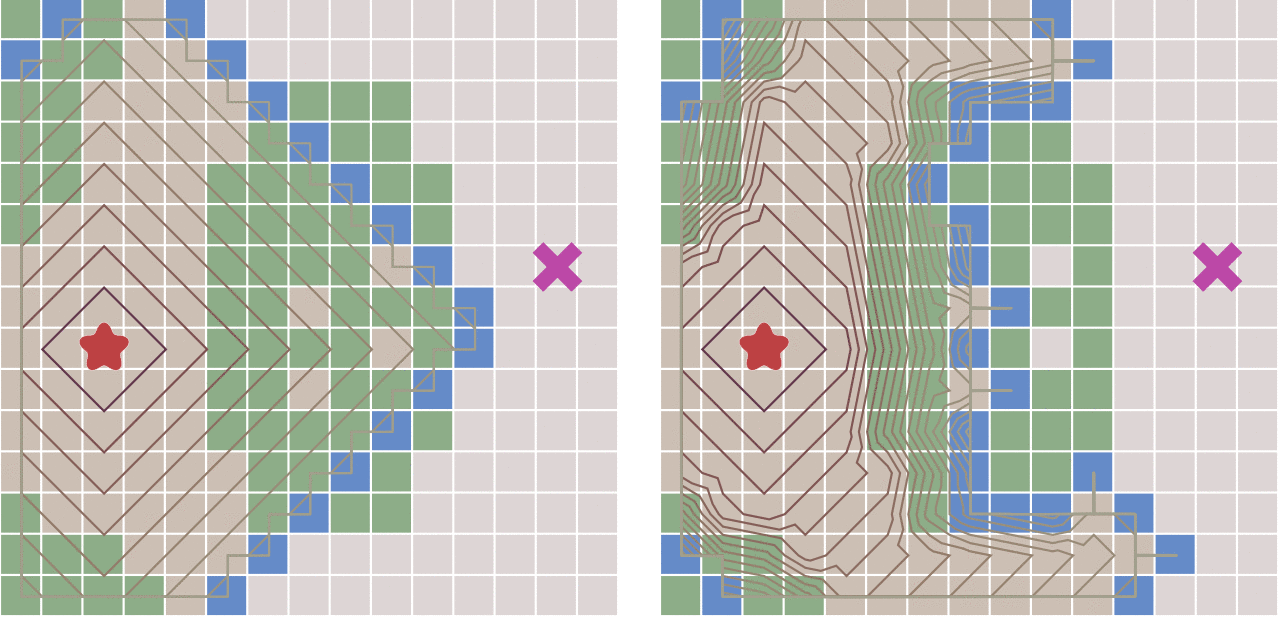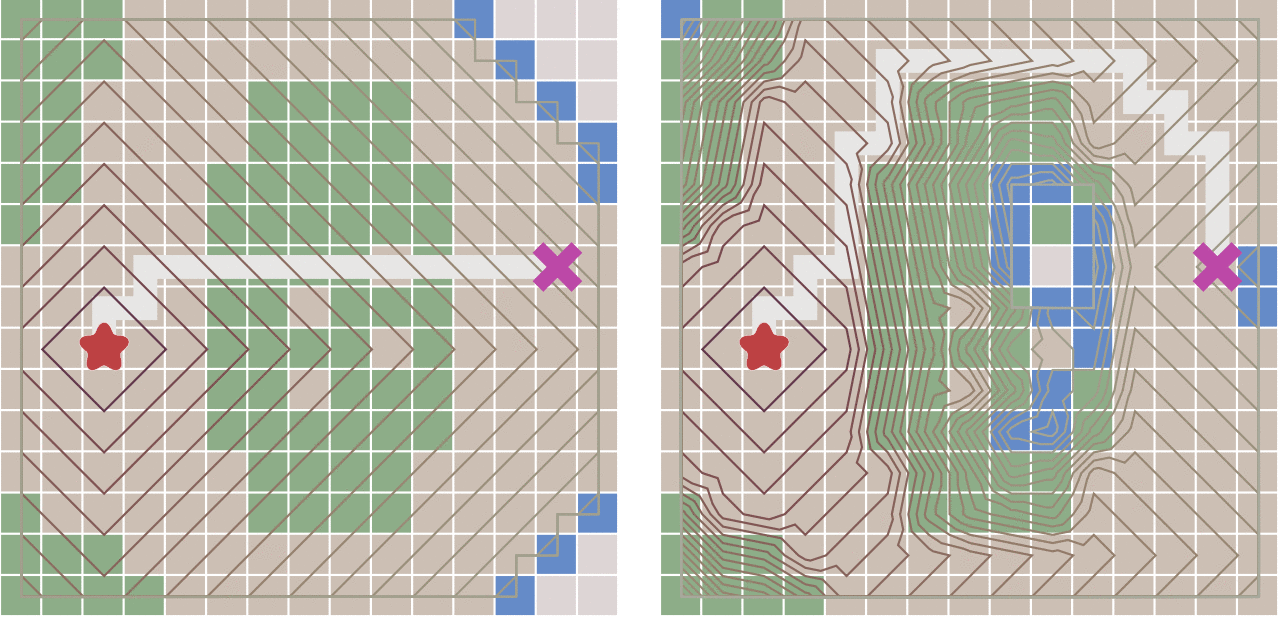
- 优点:Dijkstra 可以保证它扩展过的节点一定是从起点开始到当前的最小代价的路径,因此按照这一原则进行搜索,当它发现目标节点后,回溯出的路径一定是最小代价的路径,即具有完备性。
- 缺点:Dijkstra 不知道目标节点的位置,只能保证每一步扩展过的节点累计代价是最小的,它必须向所有方向扩展,目的性不强,算法效率不高。
最佳优先搜索(终点贪心搜索)
如果我们可以预先计算出每个节点到终点的距离,则我们可以利用这个信息更快的到达终点。
- 该算法使用一个优先队列,不过以每个节点到达终点的距离作为优先级,每次始终选取到终点移动代价最小(离终点最近)的节点作为下一个遍历的节点
- 其实就是贪心算法,每次选择走距离终点最近的节点
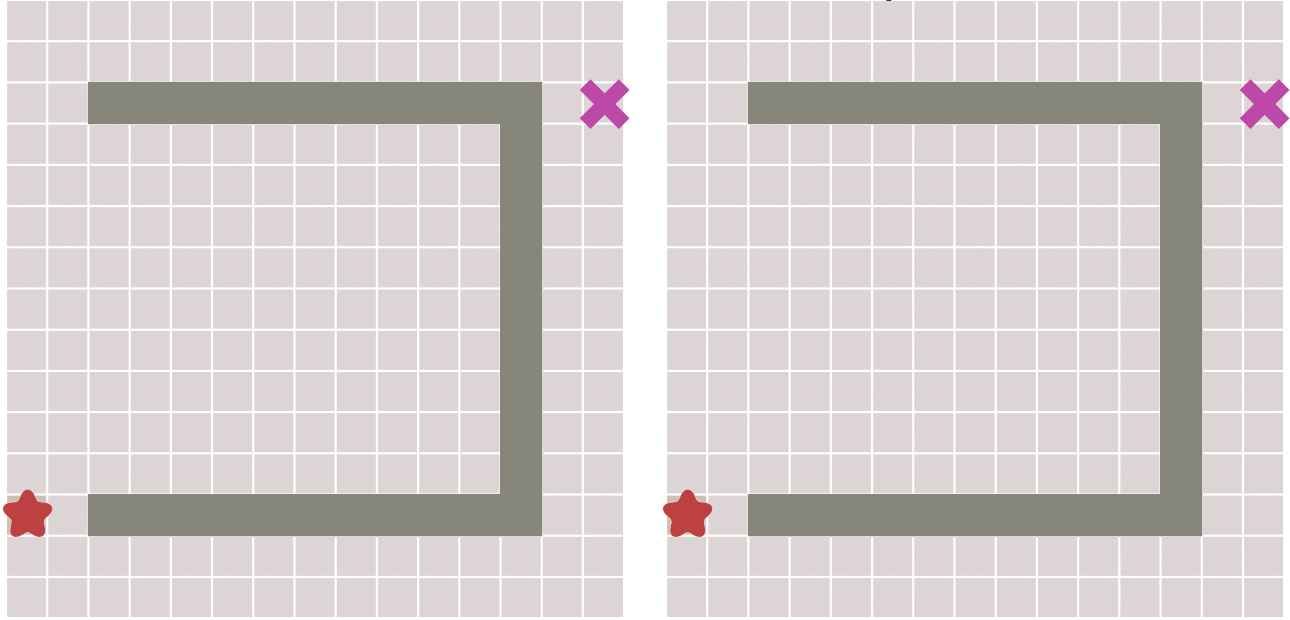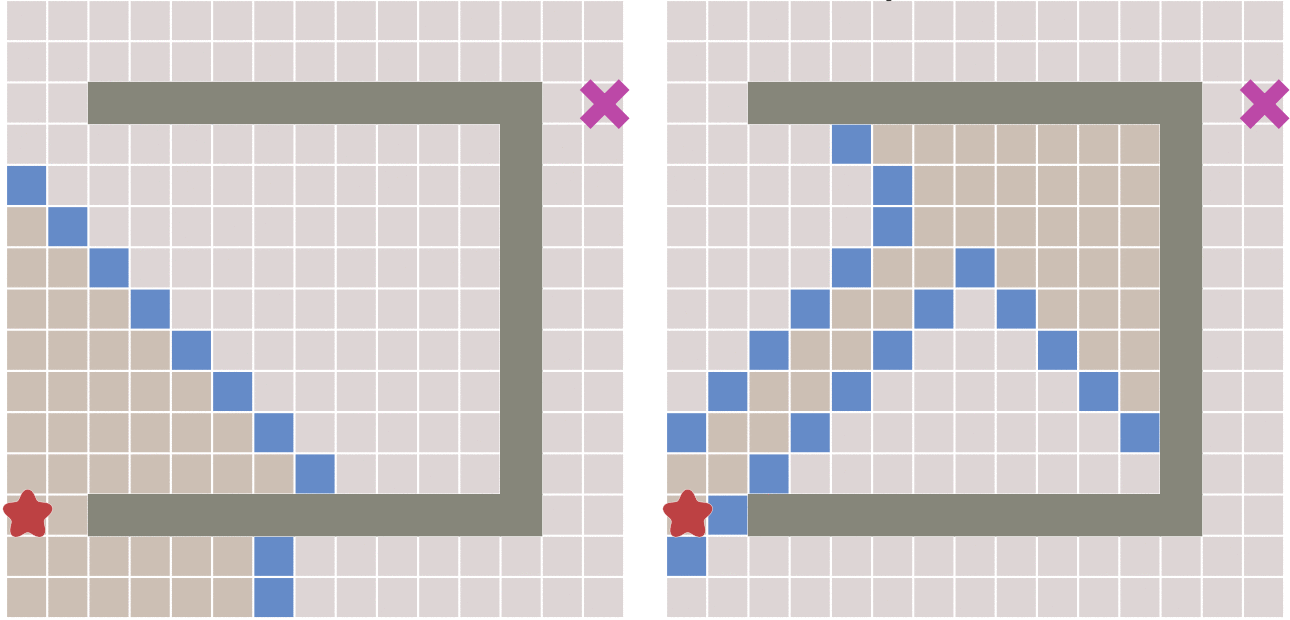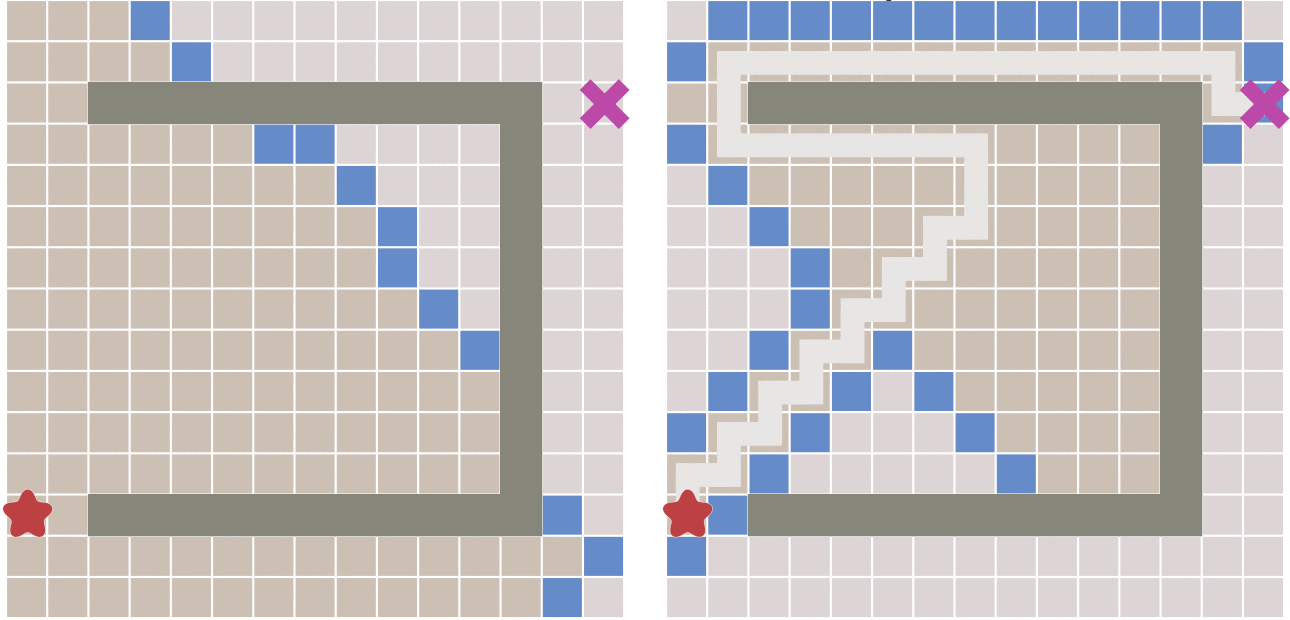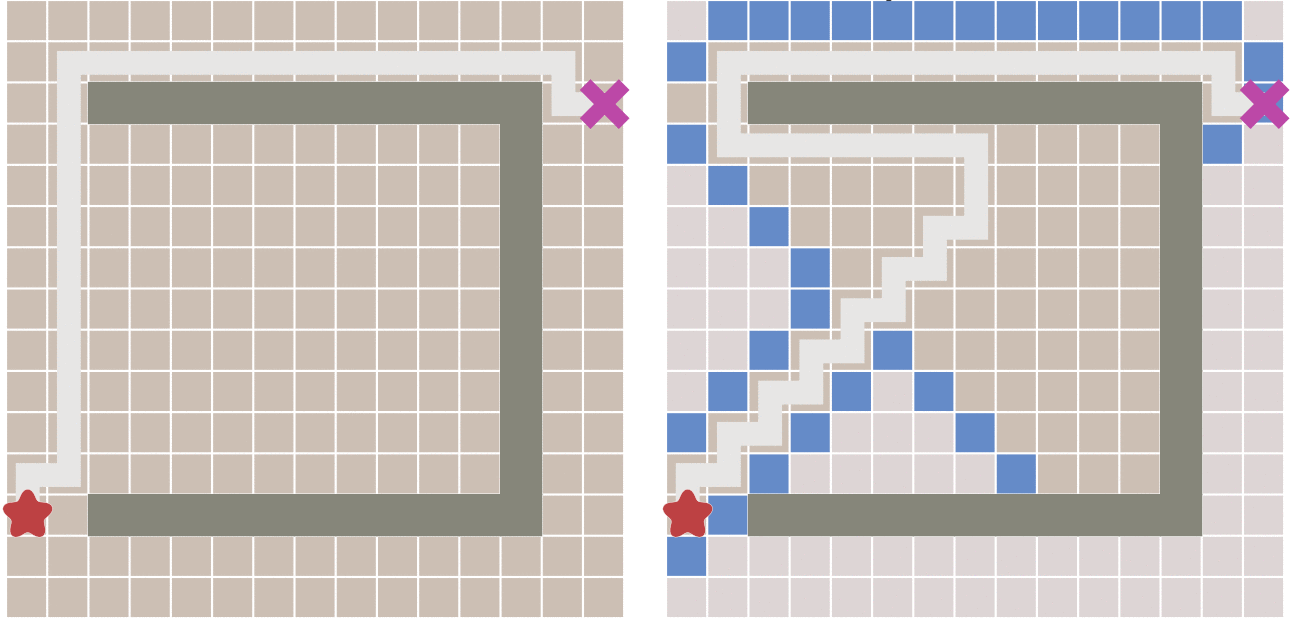
缺点:如果起点和终点之间存在障碍物,则最佳优先算法找到的很可能不是最短路径
- 右图,先走到墙边再转弯,肯定不是最短的
A* 基本原理
A Star 算法是一种常用的路径查找和图形遍历算法,它结合了 Dijkstra 算法和最佳优先搜索算法的优点,保证了最优特性的同时,加入了目标节点的信息,提升了搜索效率,该算法运行过程中每个节点的总代价 f(n) 计算方法为(也可以使用加权平均的计算方式,可以试试):
f(n)是节点 n 的总代价- 算法运行过程中,总会选取总代价最小的节点作为下一个要遍历的节点。
g(n)是节点 n 距离起点的代价- 如果
g(n) = 0,则算法退化为最佳优先搜索 -
h(n)是节点 n 距离终点的启发代价(启发函数)- 如果
h(n) = 0,则算法退化为Dijkstra
- 如果
总结一下:A* 就是一个带有启发性的 Dijkstra 算法
完备性(是否能够找到最优解)
由于采用了最佳优先搜索算法的贪心思想,所以 A* 并不能保证具有完备性(即找到最优路径),但是调整启发函数可以使得 AStar 具有完备性,来看看启发函数 h(n) 对 AStar 的影响。
启发函数的影响(完备性)
启发函数会影响 AStar 算法的行为(d(n) 节点 n 到终点的真实代价):
- 极端情况下,当启发函数
h(n)始终为 0,则将由g(n)决定节点的总代价,此时算法就退化成了Dijkstra - 如果
h(n) < d(n),则保证一定能够找到最短路径,但当h(n)的值越小,目标引导效果会越差,算法将遍历越多的节点,也就导致算法越慢。 - 如果
h(n) = d(n),则算法将保证找到最佳路径,并且速度很快(最优状态)。可惜并非所有场景下都能做到这一点,因为在没有达到终点之前,我们很难确切算出当前节点距离终点还有多远,因为中间可能存在许多障碍物遮挡 - 如果
h(n) > d(n),则算法不能保证一定能找到最短路径(因为会尽快朝着目标点搜索,如果与终点之间存在障碍物,则可能导致次优路径,类似最佳优先搜索的缺点),不过此时会很快,在尽量加速并且得到一个次优路径就可以的场景中,可以采用大的h(n) - 另一个极端情况下,如果
h(n)远大于g(n),则此时只有h(n)产生效果,这也就变成了最佳优先搜索
通过调节启发函数我们可以控制算法的速度和精确度,因为在一些情况,我们可能未必需要最短路径,而是希望能够尽快找到一个路径即可。
启发函数的计算方法
对于网格形式的图,有以下这些启发函数可以使用:
-
如果图形中只允许朝上下左右四个方向移动,则可以使用曼哈顿距离(Manhattan distance)
-
-
function heuristic(node) = dx = abs(node.x - goal.x) dy = abs(node.y - goal.y) return D * (dx + dy) - D 是指两个相邻节点之间的移动代价,通常是一个固定的常数。
-
-
如果图形中允许朝八个方向移动,允许斜着朝邻近的节点移动,则可以使用对角距离(Octagonal distance)
-
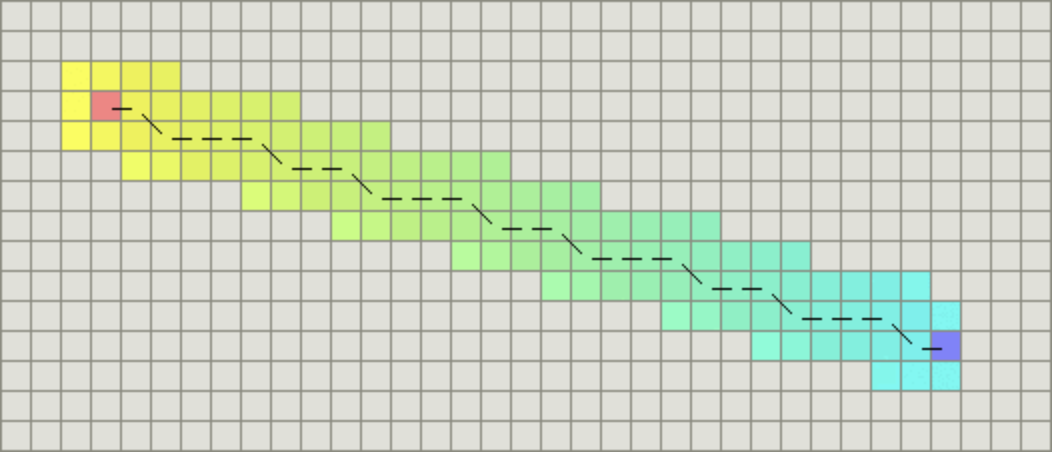
-
function heuristic(node) = dx = abs(node.x - goal.x) dy = abs(node.y - goal.y) // 这里还没看懂。。。。 return D * (dx + dy) + (D2 - 2 * D) * min(dx, dy) - D2 指的是两个斜着相邻节点之间的移动代价,如果是网格地图就为(根号 D)。
-
-
如果图形中允许朝任何方向移动,则可以使用欧几里得距离(Euclidean distance)
-
function heuristic(node) = dx = abs(node.x - goal.x) dy = abs(node.y - goal.y) return D * sqrt(dx * dx + dy * dy) - D 是指两个相邻节点之间的移动代价,通常是一个固定的常数。
-
时间复杂度
如果我们使用遍历搜索队列的办法来找到 f(n) 最小的函数,那么算法复杂度达到 $O(n^2)$,这一部分可以采用优先队列或者小根堆的办法来实现 O(nlog n) 的算法复杂度。
优缺点
- 优点:A* 算法优点在于搜索路径直接,是一种直接的搜索算法,因此被广泛应用于路径规划问题
- 缺点:
- 当 8 个邻居的代价中存在多个最小值时 A* 算法不能保证搜索到最优路径(参考优化思路)
- A* 算法并没有完全遍历所有可行解,所得到的结果不一定是最优(调整
h(n))
优化思路
核心优化思想
当存在多个相同 f(n) 的节点时,AStar 不再具有目标倾向性,会拓展没必要的节点。
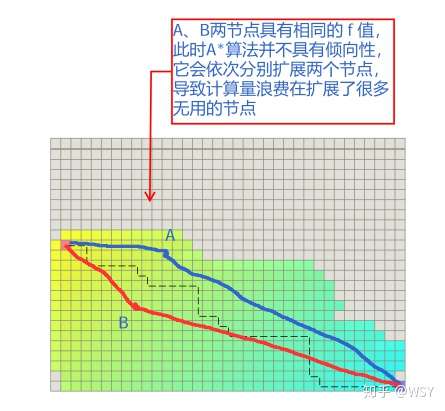
打破对称性,让 AStar 具有更强的目标倾向性,可以减少扩展没必要的节点,主要修改 h(n)
- 最简单地做法就是将
h(n)值略微放大,但此时可能有人怀疑,扩大h(n)值会不会导致h(n) > d(n),从而破坏算法的完备性?一般不会,因为真实环境中会有很多障碍物,h(n)一般远远小于d(n),所以略微放大一点不会很大地影响完备性h(n) = h(n)x(1.0 + p)
- 另一种方法:倾向于选择离起点 - 终点连线距离更近的节点,计算节点到连线的距离偏移
动态加权优化
在动态加权算法中,你假定在搜索开始时快速达到(任意)一个位置更为重要,在搜索结束时到达目标位置更为重要(动态改变目标倾向性)。
f(n) = g(n) + w(n) * h(n)
f(n) = g(n) + w(n) * h(n)
有一个权值(w >= 1 )和该启发式关联,当不断接近目标位置的时候,权重值也不断降低,这样降低了启发式函数的重要性,并增加了路径实际代价的相对重要性。
伪代码

-----------------------------------------------------
Algorithm: A* Algorithm
-----------------------------------------------------
Input: x_start, x_goal
Output: A path connecting x_start to x_goal
open_set, close_set <- init_set();
open_set.add(x_start);
while !open_set.empty() do
// 选择 F 最小,即综合优先级最高的节点
// 遍历搜索队列 O(n^2)
// 使用优先级队列或者小顶堆 O(nlogn)
cur_node <- select_minf_node(open_set);
// 到达目标即返回
if cur_node == x_goal then
break;
end
close_set.add(cur_node);
open_set.delete(cur_node);
direction <- { {0, 1}, {0, -1}, {-1, 0}, {1, 0}, {1, 1}, {-1, 1}, {1, -1}, {-1, -1}}
for i = 0 : directions do
// 计算新方向的节点,上下左右、对角
// 取决于使用的代价计算方法
new_node <- calc_new_node(cur_node, direction[i]);
// 有碰撞或者已经访问过就跳过
if !CollisionFree(new_node) or close_set.has(new_node) then
continue;
end
// 计算新方向节点的 G
new_g <- cur_node.g + ((i < 4) ? 10 : 14);
// 查找新生成的节点是否已经在 open 表中
raw_node = open_set.find(new_node.x, new_node.y);
if raw_node == null then
// 新节点不在 open 表中就加入
new_node.g <- new_g;
new_node.h <- heuristic(new_node, goal);
open_set.add(new_node);
else
// 新节点已经在 open 表中且经过 cur_node 距离起点的代价比原来更小
// 就更新父节点和 G
// H 是不变的所以不用更新
if (new_g < raw_node.g) then
raw_node.parent <- cur_node;
raw_node.g <- new_g;
end
end
end
// 反向查找路径
while cur_node != null do
path.add(cur_node);
cur_node <- cur_node.parent;
end
return path;
end
-----------------------------------------------------
相关问题
- 为何 A* 比 Dijkstra 效率高?
- A* 算法由于引入了启发函数
h(n),所以它拓展节点的时候具有一定目的性(即向目标节点的方向扩展),搜索目标节点时所需要扩展的中间节点更少,因此算法效率更高。
- A* 算法由于引入了启发函数
- 为何 A* 不具有完备性?
- 由于采用了最佳优先搜索算法的贪心思想,所以 A* 并不能保证具有完备性(即找到最优路径)
- 如何调整可以使得 A* 具有完备性?
- 当
h(n) <= d(n)时 A* 具有完备性,这里d(n)指节点 n 到目标节点的真实代价(没有看论文的证明原理)
- 当
- h(n) 的哪些计算方法满足
h(n) <= d(n),即最优性?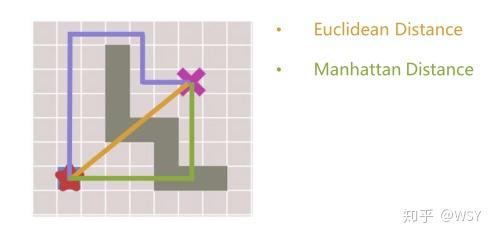
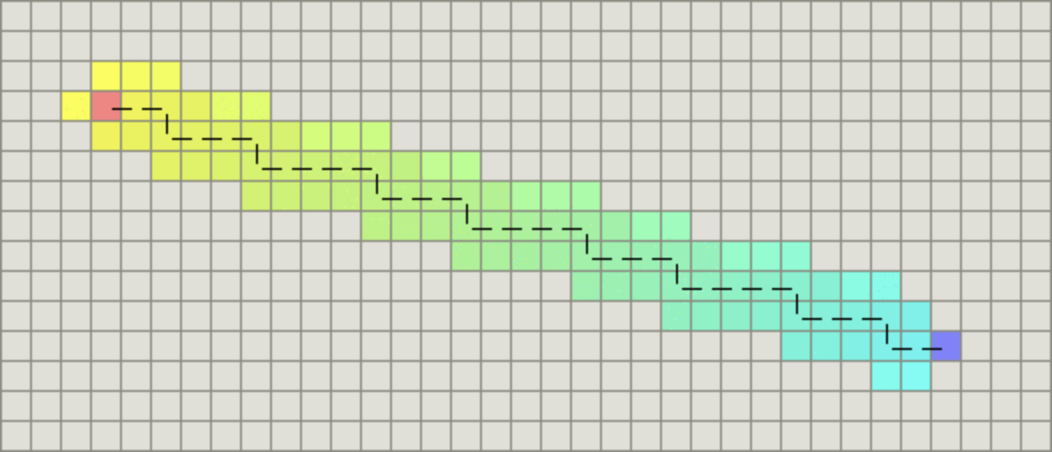
- 紫色为真实代价
d(n),黄色为采用欧式距离作为h(n)的估计代价,绿色为采用曼哈顿距离作为h(n)的估计代价- 采用曼哈顿距离作为
h(n),一定满足h(n) <= d(n) - 采用欧式距离作为
h(n),一定满足h(n) <= d(n)
- 采用曼哈顿距离作为
- 如何根据使用场景选择
h(n)- h(n) 的选择成了一个有趣的情况,它取决于我们想要
A*算法中获得什么结果 - h(n) 合适的时候,我们会非常快速地得到最短路径
- 如果 h(n) 估计的代价太低,我们仍会得到最短路径,但运行速度会减慢
- 如果估计的代价太高,我们就放弃最短路径,但
A*将运行得更快
- h(n) 的选择成了一个有趣的情况,它取决于我们想要
本文非原创,整理自以下的参考博客:
- https://zhuanlan.zhihu.com/p/54510444
- https://www.jianshu.com/p/9f911f44913b
- https://wenwen.sogou.com/z/q710269711.htm
- https://paul.pub/a-star-algorithm/
- https://zhuanlan.zhihu.com/p/61633289
- https://howardlau.me/programming/a-star-algorithm.html
- https://zhuanlan.zhihu.com/p/104051892
- https://kimmykuang.gitbooks.io/algorithm-share-pahf/content/lists/routing/astar/astar_optimize.html
本文原创首发于微信公号「登龙」,分享机器学习、算法编程、Python、机器人技术等原创文章,扫码即可关注!

DLonng at 04/12/21

