自动驾驶规划算法 - ROS Teb 局部轨迹优化原理
版权声明:本文为 DLonng 原创文章,可以随意转载,但必须在明确位置注明出处!
1 Teb 方法概述
TEB 全称 Time Elastic Band(时间弹性带)Local Planner,该方法针对全局路径规划器生成的初始全局轨迹进行后续修正,从而优化机器人的运动轨迹,属于局部路径规划。在轨迹优化过程中,该算法拥有多种优化目标,包括但不限于:整体路径长度、轨迹运行时间、与障碍物的距离、通过中间路径点以及机器人动力学、运动学以及几何约束的符合性。
TEB 被表述为一个多目标优化问题,大多数目标都是局部的,只与一小部分参数相关,因为它们只依赖于几个连续的机器人状态。这种局部结构产生了一个稀疏的系统矩阵,使得它可以使用快速高效的优化技术,例如使用开源框架 g2o 来解决 TEB 问题。
通俗的解释就是 TEB 生成的局部轨迹由一系列带有时间信息的离散位姿(pose)组成,g2o 算法优化的目标即这些离散的位姿,使最终由这些离散位姿组成的轨迹能达到时间最短、距离最短、远离障碍物等目标,同时限制速度与加速度使轨迹满足机器人的运动学。
需要指出的是 g2o 优化的结果并非一定满足约束,即实际都是软约束条件,若参数设置不合理或环境过于苛刻,teb 都有可能失败,规划出非常奇怪的轨迹。所以在 teb 算法中包含有冲突检测的部分,在生成轨迹之后逐点判断轨迹上的点是否与障碍物冲突,此过程考虑机器人的实际轮廓。
2 Teb 基本原理
Eletic Band
连接起始、目标点,并让这个路径可以变形,变形的条件就是将所有约束当做橡皮筋的外力。

Time Eletic Band
起始点、目标点状态由用户的全局规划器指定,中间插入 N 个控制橡皮筋形状的控制点(机器人姿态)。为了显示轨迹的运动学信息,我们在点与点之间定义运动时间 Time,即:
Time + Elastic Band = Timed Elatics Band
下面就来定义一条时间弹性带 TEB,首先定义机器人位姿,每个位姿称为一个 configuration:
\(X_i = (x_i, y_i, \beta_i)^T\)
则由 configuration 组成的序列为:

然后将两个 configuration 间的时间间隔定义为 $\Delta T_i$,表示机器人由一个 configuration 运动到下一个 configuration 所需的时间,组合成时间序列 $\tau$:

最后将 configuration 序列和时间间隔序列合并得到一个时间弹性带序列对象 $B$:
\(B = (Q, \tau)\)

这个序列对象 $B$ 就是我们后面要优化的变量,他表示了一条经过 TEB 算法优化过后的局部轨迹。
目标函数
时间弹性带定义完后,我们需要定义要优化的目标函数,TEB 通过加权多目标优化方法获取最优的序列 $B$:

其中 $B*$ 为最优结果,$f(B)$ 为考虑各种约束的加权多目标函数(是一个非线性最小二乘问题,所以可以用 g2o 构建超图利用 LM 求解),$f_k$ 为每个目标函数的权值。 在此应注意,每个目标函数只与时间弹性带中的某几个连续状态有关,而非整条弹性带中所有状态,因此是对稀疏矩阵模型进行优化。
约束条件
1. 路径跟随约束
跟随路径将 TEB 拉向初始的全局路径,跟随路径以 configuration 距全局路径的允许的最大距离 $r_{p_{max}}$作为约束,$d_{min,j}$ 为 configuration 序列到全局路径的最近距离:


2. 避障约束
避障约束使得 TEB 远离障碍物,避障目标以 configuration 距障碍物的允许的最小距离 $r_{o_{min}}$ 作为约束,$d_{min,j}$ 同时也表示 configuration 序列到障碍物的最近距离:


3. 速度,加速度动力学约束
机器人运动的平均线速度和角速度可以通过相邻的 configuration $X_i, X_{i + 1}$ 和时间间隔 $\Delta T$ 计算得到:

线速度约束可以表示为: \(f_{v_i} = e_{\tau}(v_i,v_{max},\epsilon, S, n)\)
机器人的平均线加速度用同样的近似计算得到:

角加速度计算类似,以差动机器人为运动模型为例,两轮的转速可通过以下计算得到:

其中 L 为两轮轴距的一半,对上面 2 个式子作关于时间的微分即可得到两轮的角加速度。
4. 非全向运动学约束(没有推导该公式)
差动机器人在平面运动只有两个自由度,其只能以朝向的方向直线运动或旋转。这种运动学约束使得机器人以有若干弧段组成的平滑的轨迹运动,则相邻的两个 configuration 应在弧段的两端:

则 $X_i$ 与运动方向的夹角 $\theta_i$ 与 $X_{i + 1}$ 与运动方向的夹角 $\theta_{i+1}$ 相同: \(\theta_i = \theta_{i+1}\) 则推出:

运动方向向量为:

进而得到运动学约束的目标函数:

5. 最快路径约束
时间约束的目标函数即为最小化时间间隔序列的二次方:

求解方法
稀疏矩阵优化模型
TEB 被表述为一个多目标优化问题,大多数目标都是局部的,只与一小部分参数相关,因为它们只依赖于几个连续的机器人状态。这种局部结构产生了一个稀疏的系统矩阵,使得它可以使用快速高效的优化技术,例如使用开源框架 g2o 来解决 TEB 的优化问题。
Hyper-Graph 问题建模
TEB 优化问题可以转化为 Hyper-Graph 问题:

configurations 和时间间隔作为 nodes,约束函数为 edges,各 nodes 由 edges 连接起来构成 Hyper-Graph,该图中每一个约束都为一条 edge,并且每条 edge 允许连接的 nodes 的数目是不受限制的。
下面左图展示了 2 个configurations $(s_0, s_1)$,一个时间间隔 $\Delta T_0$ 和一个障碍物 $o_1$ 组成的 Hyper-Graph。速度约束需要计算平均速度,则该约束的边与 $(s_0, s_1)$ 和 $\Delta T_0$ 有关,因此该 edge 将这 3 个 nodes 连接起来。障碍物约束将障碍物和离障碍物最近的 configuration 连接起来,因为障碍物点是固定的,算法不应也不能对其位置进行优化。右图是一个更加复杂的 Hyper-Graph。

g2o 框架
g20 是通用图优化(General Graph Optimization)库,g2o 的核里带有各种各样的求解器,而它的顶点、边的类型则多种多样,通过自定义顶点和边(TEB 把 configuration 和 $\Delta T_i$ 当作顶点,约束函数当作边,代码内部自定义了这 2 个类型),事实上只要一个优化问题能够表达成图,那么就可以用 g2o 去求解它,g2o 代码框架如下:
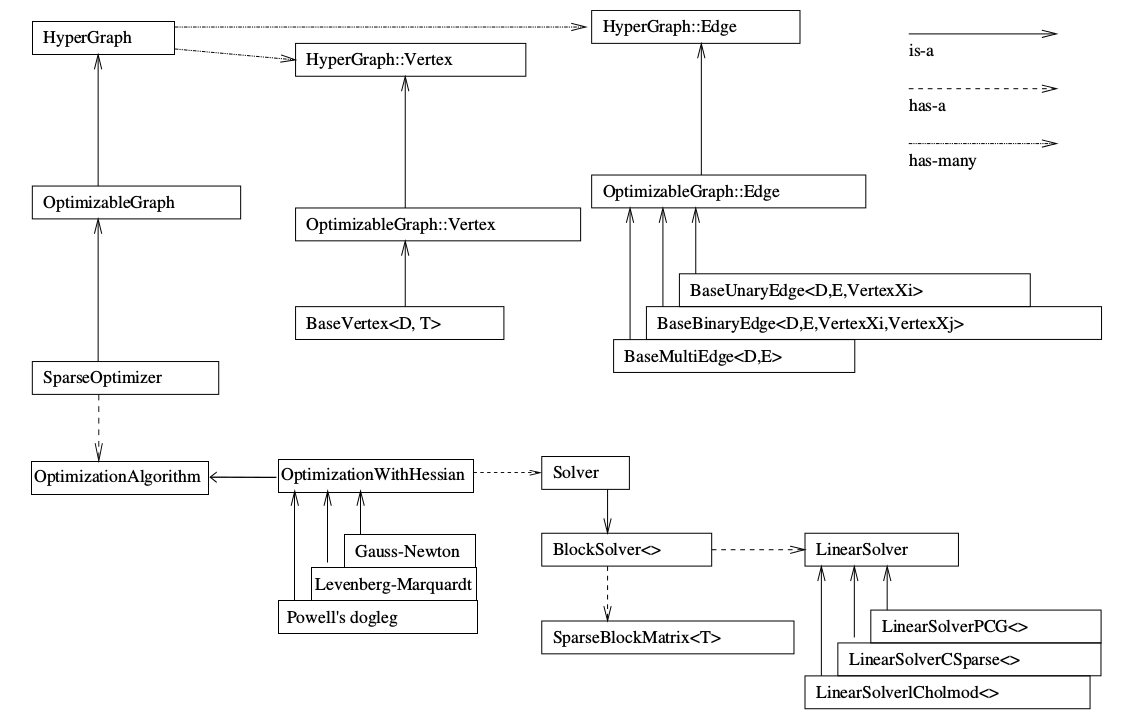
在 g2o 中选择优化方法一共需要三个步骤:
- 选择一个线性方程求解器,从 PCG, CSparse, Choldmod 中选,TEB 使用 CSparse。
- 选择一个 BlockSolver。
- 选择一个迭代策略,从GN, LM, Doglog 中选,TEB 使用 LM。
g2o 求解超图问题的原理
如果目标函数可以转为求解非线性最小二乘问题,则可以构建对应的超图,然后利用 LM 求最小二乘问题的解。
3 代码框架
代码优化流程

大致流程是:
- 先对全局规划器规划出的 global_plan 进行一些预处理,包括截取部分路径、转换坐标系,然后更新 via_points(在全局路径上等间隔选出)
- 更新障碍物信息(若使用 costmap_converter 插件,可以将障碍物做一定的简化,简化为线段、多边形等,可在一定程度上提高规划效率)
- 开始构建超图,添加顶点和约束边
- 开始优化
- 优化完毕后需要检查轨迹是否无碰撞
- 根据 TEB 前 2 个
configuration的位姿和时间间隔计算要发送到地盘的线速度和角速度
并行优化类
teb_local_planner 包中实现了两种规划器,一个就是普通的 TebOptimalPlanner,另一个是 HomotopyClassPlanner,HomotopyClassPlanner 是一种同时优化多个轨迹的方法,由于目标函数的非凸性会生成一系列最优的候选轨迹,最终在备选局部解的集合中寻求总体最佳候选轨迹。
本文原创首发于微信公号「登龙」,分享机器学习、算法编程、Python、机器人技术等原创文章,扫码即可关注!

DLonng at 03/14/21
