从 0 开始机器学习 - 机器学习基本概念

一、机器学习的定义

顾名思义就是让机器像人类一样会学习，比如熟悉房子的人能根据房屋面积、地段、楼层等特征给出一个房屋的价格，这是我们人类通过学习以往的经验得到的结果。

其实对于机器来说，这个过程也是类似的，只不过我们的大脑需要用算法来代替。我们定义一个带未知参数的函数 $y = ax + b$，然后再找一些房屋面积等数据$(x, y)$，把这些数据挨个输入到函数里面进行参数计算，然后再用一些优化手段来计算出这个函数的最优参数$(a, b)$，最后的结果就是得到一个确定的函数，比如：$y = 2x + 10$。

接着我们就可以用这个函数来预测未知的房屋价格：未知房屋价格 = 2 * 未知房屋的面积 + 10，比如输入面积 50 平方，输出价格为 110 万，这就机器学习算法给出的预测结果。

一个比较学术的定义由来自卡内基梅隆大学的 Tom Mitchell 提出，定义如下：

一个程序被认为能从经验 E 中学习，解决任务 T，达到性能度量值 P，当且仅当，有了经验 E 后，经过 P 评判，程序在处理 T 时的性能有所提升。

比如以下棋的机器学习算法为例：经验 E 就是程序上万次的自我练习的经验，任务 T 是下棋，性能度量值 P 是它在与一些新的对手比赛时，赢得比赛的概率。

二、监督学习

监督学习可以理解为：算法使用的数据集中已经人为设置了正确的属性。

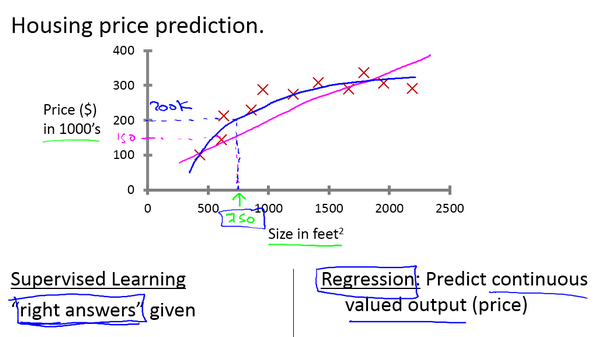
比如用监督学习来根据房屋面积预测房价，那么在训练数据集中每个房屋面积都对应一个确定的价格（750, 200），这个确定的价格 200 就是我们人为给定的，用来训练算法模型（预测函数参数）。

三、无监督学习

无监督学习：算法使用的数据集不做任何人为处理，即没有加上任何属性。

比如这个例子用年龄和使用电脑的时间来将老师和学生群体分来，输入的数据只有（年龄，使用电脑的时间），是不含有的对应的群体标签的，我们最后要用无监督的机器学习算法来区分这两个群体：

在无监督学习中，常用的是聚类算法，即把距离相近的数据点划分为同一个簇，比如 Google 新闻从互联网上收集很多条新闻，然后将类型相近的文章划分为同一个类别：科技，情感，政治等等。

四、机器学习问题类型

4.1 回归问题

回归问题：预测连续的输出（拟合函数曲线），比如根据房屋面积预测房价就是典型的回归问题：

回归问题的本质就是用已有的数据计算出拟合原数据效果函数曲线的表达式，然后用这个曲线来预测一个输入的输出，上图房价问题通过不断的优化函数模型和参数，可以看出蓝色的曲线比紫色的直线拟合（回归）效果好。

判断问题类型：

你有一大批同样的货物，想象一下，你有上千件一模一样的货物等待出售，这时你想预测接下来的三个月能卖多少件？ - 回归问题

4.2 分类问题

分类问题：预测离散的数据点。比如下面的二分类问题：

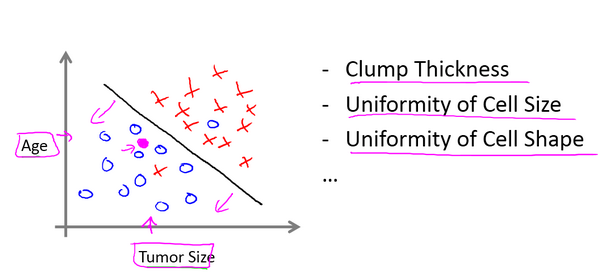
红×和蓝圈代表两种不同类型，中间的直线是我们算法预测的分类边界函数，当函数参数确定好了，我们给定一个输入，那么输出就是在直线上部或者下部的一个离散的点，表示该输入数据是最可能是哪一种类型，对于多个特征的分类问题，原理是一样的。

比如红 X 代表苹果，蓝圈代表橘子，我们把一个水果图像输入该算法，如果算法的输出在直线的右上方（红 X），那么该图像上是苹果的概率比较大，如果算法的输出在左下方（蓝圈），则说明是橘子的概率比较大。

分类问题的输出可以是二分类或者多分类。

判断问题类型：

你有许多客户，这时你想写一个软件来检验每一个用户的账户。对于每一个账户，你要判断它们是否曾经被盗过？

五、机器学习算法工作流程

以预测房价的监督学习为例：

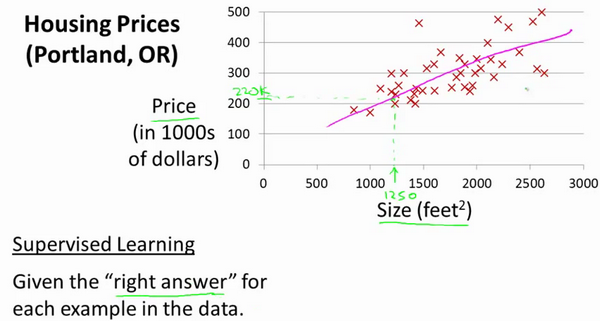
一个机器学习算法的工作流程基本如下：

5.1 确定训练数据集

训练数据集如下，输入是房屋面积，输出是房屋价格，因为是监督学习，所以房屋价格就是标签值：

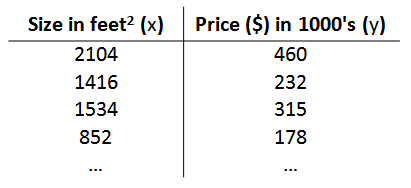
5.2 选择模型

直接把模型理解为函数即可，选择模型就是选择一个函数，比如上面的房价数据，直观来看用一个直线 $h(x) = ax +b $ 就能够挺好的拟合，所以这里选择的模型就是这个直线函数。

不要觉得模型这个字很高大上，把它理解成一个函数即可，这个函数又叫做假设函数，通常用 $h(x)$ 表示。

5.3 训练模型

训练模型就是为了确定最优的函数参数，比如我们来训练预测房价的模型 $h(x) = ax + b$ ，训练的过程就是求最优的 $a, b$ ，把最优的值求出来，那么我们对模型的训练就结束了。

那么我们如何来衡量每组参数对模型拟合的效果呢？交给代价函数！

5.3.1 代价函数

代价函数 $Cost Function$ 是用来评估当前参数对应的模型对训练集拟合的效果，如果代价函数的值比较小，则拟合误差小，效果好，如果代价值很大，则拟合效果不好：

那么有了衡量参数效果的代价函数后，为了使得拟合效果尽可能好，我们需要求代价函数的最小值，如何求呢？学习算法！

5.3.2 学习算法

终于到了关键的一步，使用学习算法来求出代价函数的最小值，当求出最小值后，就可以得到代价函数最小值对应的参数，比如 $a = 1, b = 50$，是使得代价函数取最优值的模型参数，当求出最优参数时训练就结束了。

常用的一个学习算法是梯度下降法，后面会带大家一步一步推导它的公式。

5.4 预测

有没有发现我们前面费了好大功夫就求出了 $a = 1, b = 50$，模型也即 $h(x) = x + 50$，现在就可以用这个模型来预测新的房屋的价格了，比如一个未知的样本房屋面积为 50 平方，带入训练好的模型中：

\[h(50) = 1 * 50 + 50 = 100 万\]

预测结果显示该模型对 50 平方的房屋给出的价格为 100 万，这就完成了模型的预测任务啦！

5.5 如何评价预测效果

预测结果是得到了，可是预测的效果如何呢？在实际工程应用中，求出答案往往不是最终目的，得到最好的效果才是我们的目标。

为了评估机器学习模型对未知样本的预测效果，我们用一些评价指标即可以百分比的量化方式评估模型预测能力，比如查准率，召回率和 F1-Score，这些后面会详细总结，这里主要以了解为主。

OK！今天就跟大学分享了我对机器学习基本概念的一些理解，打好基础是后续学习的关键，你学会了吗？

本文原创首发于微信公号「登龙」，分享机器学习、算法编程、Python、机器人技术等原创文章，扫码即可关注！