从 0 开始机器学习 - 一文入门多维特征梯度下降法！

版权声明：本文为 DLonng 原创文章，可以随意转载，但必须在明确位置注明出处！

今天登龙跟大家分享下我对多维特征的读取、缩放和多变量梯度下降算法的理解，文章不长，有理论也有实际的代码，下面开始，Go！

一、如何表示多维特征？

1.1 特征缩放

实际项目中在读取多维特征之前需要先对数据进行缩放，为什么呢？

因为在有了多维特征向量和多变量梯度下降法后，为了帮助算法更快地收敛，还需要对选用的特征进行尺度缩放，其实就是缩小特征值，将多个特征的值都缩小到同样大小的区间，通常是缩小到 [-1, 1] 周围，以下图为例：

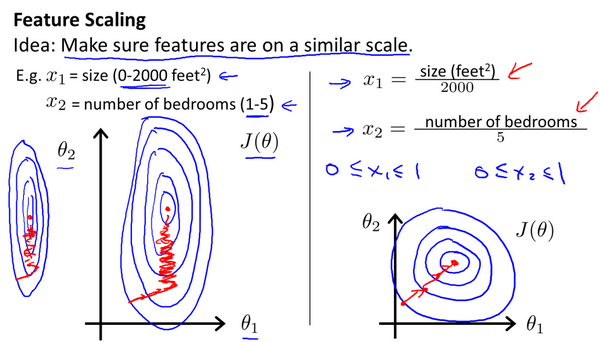
在没有进行特征缩放之前，两参数梯度下降的等高线图呈竖的椭圆形，这是因为横轴和纵轴参数范围不同，进而导致算法在寻找最小值时会迭代很多次，而当进行缩放使得横纵轴范围大致相同后，等高线图基本呈圆形，算法在迭代的时候往一个方向很快就能找到最小值，大大减少迭代次数。

缩放的最终结果不一定非要准确到 [-1, 1]，比如 [-3, 3]，[-2, 1] 这些范围不是太大都是可以的，一个又常用有简单的特征缩放计算方法是：

\[x_n=\frac{x_n - \mu_n}{s_n}\]

其中 ${\mu_{n}}$ 是平均值，${s_{n}}$ 是（max - min），比如用这个公式将所有的房屋面积和卧室数量进行缩放：

$x_1 = (size - 1000) / 2000$，其中 1000 是面积平均值，2000 是最大面积减最小面积。
$x_2 = (bedrooms - 2) / 5$，其中 2 是卧室数量平均值，5 个最大卧室数量减去最小卧室数量。

理论学会后，再来学习下实际的特征缩放代码：

# 特征缩放
def normalize_feature(df):
    # 对原始数据每一列应用一个 lambda 函数，mean() 求每列平均值，std() 求标准差
    return df.apply(lambda column: (column - column.mean()) / column.std())

我们用这个函数来实际缩放一下含有 2 个特征的原始房价数据：

# 读取原始数据
raw_data = pd.read_csv('ex1data2.txt', names = ['square', 'bedrooms', 'price'])

# 显示前 5 行
raw_data.head()

# 对原始数据进行特征缩放
data = normalize_feature(raw_data)

# 显示缩放后的前 5 行数据
data.head()

可以看到缩放后的数据范围基本都在 $[-1, 1]$ 区间左右，说明我们的特征缩放成功了 ^_^！下面来学习如何读取多维特征！

1.2 读取多维特征

还记得上篇文章我们介绍的第一个机器学习算法吗？即通过房屋面积来预测价格，这个问题中只使用一个输入特征房屋面积，可现实生活中要解决的问题通常都含有多个特征，并且用多个特征训练出的模型准确度更高，那么如何机器学习算法如何处理多个特征的输入呢？

我们还用预测房价的例子，不过这次要增加另外 3 个特征，卧室数量，房屋楼层，房屋年龄：

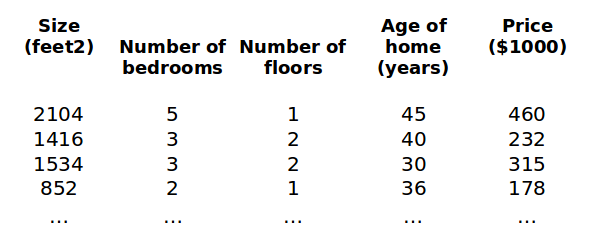
这样一来，我们就有了 4 个输入特征了，特征多了，表示的方法也要升升级了：

$n$：输入特征的数量，即特征矩阵列数，也即特征向量的维度
${x^{\left( i \right)}}$：训练集中第 $i$ 个实例向量，就是特征矩阵的第 $i$ 行，比如列向量 ${x}^{(2)}\text{=}\begin{bmatrix} 1416 & 3 & 2 & 40 \end{bmatrix}^T$
${x_j}^{\left( i \right)}$：训练集中第 $i$ 个实例的第 $j$ 个特征，比如 $x_2^{\left( 2 \right)}=3$

特征数量增加了，之前的假设函数肯定也需要修改，要把增加的特征变量和参数加上：$h_{\theta}\left( x \right)={\theta_{0}}+{\theta_{1}}{x_{1}}+{\theta_{2}}{x_{2}}+…+{\theta_{n}}{x_{n}}$，虽然这样表示没问题，但是却不方便利用向量来计算，因为参数 $\theta$ 有 n + 1 个，但 $x$ 只有 n 个，那怎么办呢？

很简单，我们额外增加一个 ${x_0}=1$，则上式变为：

\[h_{\theta} \left( x \right)={\theta_{0}}{x_{0}}+{\theta_{1}}{x_{1}}+{\theta_{2}}{x_{2}}+...+{\theta_{n}}{x_{n}}\]

这样一来就可以写成向量相乘的形式：

\[h_{\theta} \left( x \right)={\theta^{T}}X\]

你可能要问了为何要写成向量的形式？主要因为 2 点：

使用向量方便程序编写，一句计算特征向量的代码就可以同时计算多个输入参数，因为一个特征向量中包含所有输入参数
使用向量方便算法执行，梯度下降算法要求参数同时更新，如果不使用向量，那更新起来非常麻烦。

通过增加一个维度 $x_0 = 1$，最终训练集的特征矩阵的大小为：$m * (n + 1)$，其中 m 为行数，n + 1 为列数。

那来看下读取多维数据并添加一列全 1 向量的函数代码：

# 读取原始数据，返回 m * (n + 1) 维特征矩阵
def get_X(df):
    # 创建 m 行 1 列的数据帧
    ones = pd.DataFrame({'ones': np.ones(len(df))})
    
    # 合并全 1 向量作为元素数据第一列，axis = 0 按行合并，anix = 1 按列合并
    data = pd.concat([ones, df], axis=1)
    
    # 返回特征矩阵
    return data.iloc[:, :-1].values

为了简单点，这里假设原始房价数据只有 2 个输入特征，即房屋面积和卧室数量：

我们用上面的函数来读取下数据特征到向量 X：

# 读取原始数据，增加第一列全 1 向量
X = get_X(data)

# 输出数据、维度和类型
print(X.shape, type(X))
print(X)

输出结果如下：

# 47 行，3 列 = 47 * (2 + 1)
(47, 3) <class 'numpy.ndarray'>

可以看到特征矩阵的第一维列向量全为 1，后两列不变（数据换成科学计数法表示），这与我们上面介绍的对多维特征的操作方法结果相同！读取多维特征之后，我们就可以将特征矩阵 X 的每一行作为一个特征向量（就是特征组成的向量 =_=），并用它们来训练机器学习算法啦！

以上就是我对多维特征作为机器学习算法输入的一些理解，非常感谢吴恩达老师的公开课 ^_^。上面的代码都在文末我的 Github 仓库，直接下载就能运行，记得给我个 star 哦！

二、多变量梯度下降法

多维特征读取后，就可以学习多变量梯度下降法了，其实与上一篇博客的单变量梯度下降原理是一样的，只不过增加了特征变量，相应地参数也就增加了。

比如线性回归的多变量假设函数、代价函数、梯度下降法分别如下：

假设函数：$h_{\theta}\left( x \right)=\theta^{T}X={\theta_{0}}+{\theta_{1}}{x_{1}}+{\theta_{2}}{x_{2}}+…+{\theta_{n}}{x_{n}}$
代价函数：$J \left( \theta_0, \theta_1 … \theta_n\right) = \frac{1}{2m}\sum\limits_{i=1}^m \left( h_{\theta}(x^{(i)})-y^{(i)} \right)^{2}$
多变量梯度下降法

因为参数增加到 n 个，所以梯度下降的偏导数也要分别对每个参数求一次，然后同时更新 n 个参数：

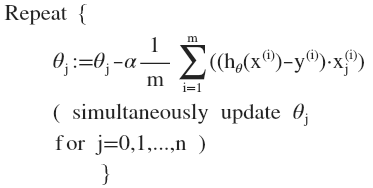
比如当 $n>=1$ 时更新前 3 个参数：

我觉得挺好理解的，只需要按照单变量梯度下降的逻辑拓展下变量和参数的数量即可，前提一定要完全理解单变量的梯度下降。

那继续来看下多变量梯度下降的算法代码，与单变量梯度下降一毛一样，先计算偏导数：

# 计算偏导数
def gradient(theta, X, y):
    m = X.shape[0]
    
    inner = X.T @ (X @ theta - y)
    
    return inner / m

再迭代下降：

# 批量梯度下降
# epoch: 下降迭代次数
# alpha: 初始学习率
def batch_gradient_decent(theta, X, y, epoch, alpha = 0.01):
    # 计算初始成本：theta 都为 0
    cost_data = [lr_cost(theta, X, y)]
    
    # 创建新的 theta 变量，不与原来的混淆
    _theta = theta.copy()
    
    for _ in range(epoch):
      	# 新的 theta = 旧的 theta - 学习率 * 偏导数
        _theta = _theta - alpha * gradient(_theta, X, y)
        # 累加成本数据，用于可视化
        cost_data.append(lr_cost(_theta, X, y))
        
    return _theta, cost_data

来调用下这个梯度下降函数，初始学习率 alpha 设置为 0.01，迭代 epoch = 500 次：

final_theta, cost_data = batch_gradient_decent(theta, X, y, epoch, alpha = alpha)

这是最终的成本和迭代次数的曲线，可以看到成本 cost 最终基本趋于不变，说明梯度下降算法收敛啦！

话说我之前忘记讲解单变量梯度下降的代码了，下次一定补上！文章内的代码仓库：

https://github.com/DLonng/AI-Notes/blob/master/MachineLearning/code/ex1-linear%20regression/multi_feature.ipynb

OK，今天就跟大家分享这些，喜欢的小伙伴记得关注下面的公众号，持续关注我哦！

本文原创首发于微信公号「登龙」，分享机器学习、算法编程、Python、机器人技术等原创文章，扫码即可关注！